Fake Refraction in DX7
Back when the Geforce 1 first came out (around May, 2000) I
wrote a demo on how to use cube-maps to fake refractions.
There is a paper is available in word
document or PDF file format.
Approximating Refraction
Problem
Statement
Refraction is a phenomenon that simulates the bending
of light rays through semi-transparent objects.
Refraction can make a 3d graphics scene look much more realistic.
Real world objects can both reflect and refract light waves to distort
images seen through them. There are
several properties defined with refraction, Snell's law and the critical angle.
Snell's law states that for a light ray going from a less dense medium to
a higher dense medium, the light ray will bend in one direction and going from a
higher density medium to a lower density medium, it will bend in the other
direction. These properties are
known as the refraction index and it is a ratio of the speed of light through
one medium divided by the speed of light through the other medium.
Snell's Law
Snell's law states that a light is traveling low
index to a high index (e.g. air is a low index and glass is a high index), the
light ray will be bent toward the normal. On
the other hand if light is traveling from a high index to a low index (e.g.
glass to air), the light will bend away from the normal.
Here is a diagram of Snell's law.
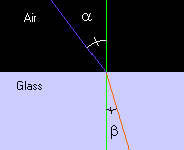
The purple line represents a light ray coming hitting
a glass object and you can see that according to Snell's law that the light
would bend towards the normal in this case (the red line).
Mathematically speaking Snell's law is stated as:
n1 * sin(a)
= n2 * sin(b) where
n1 and n2 are the index of refraction for each medium.
If you reverse the sense of the light direction, you
can see that if the light were the red line and the light were traveling from
the glass to air, it would bend away from the normal of the surface.
Snell also stated that the angles between the
incident ray and the normal of the surface and the outgoing ray's angle in
regards to that normal could be expressed in terms of a ratio.
This ratio is specified as the speed of light through the medium as
compared to the speed of light through a vacuum.
If the speed of light through a vacuum is expressed as 1.0, all other
mediums are expressed as a ratio of the speed of light compared to a vacuum.
Here is a short list of refraction index of materials
Material |
Refraction Index |
|
Vacuum
|
1.00000
|
|
Air
|
1.00029
|
|
Alcohols
|
1.32900
|
|
Crown
Glass
|
1.53000
|
|
Crystal
|
2.00000
|
|
Diamond
|
2.41700
|
|
Emerald
|
1.57000
|
|
Fused
Quartz
|
1.46000
|
|
Heavy
Flint Glass
|
1.65000
|
|
Glass
|
1.50000
|
|
Ice
|
1.30900
|
|
Quartz
|
1.64400
|
|
Ruby/Sapphire
|
1.77000
|
|
Salt
|
1.54400
|
|
Sugar
Solution (80%)
|
1.49000
|
|
Sugar
Solution (30%)
|
1.38000
|
|
Topaz
|
1.61000
|
|
Water
|
1.33333
|
Snell's law simply states that given an incident ray
at an angle relative to the normal of a surface, that ray will change angle
based on the refraction index, which is simply a ratio to reduce/increase the
angle by after the ray passes from one medium to another.
So if it is assumed that we are going from a vacuum
(which is close to the refraction index of air) to water and we know the
incident angle and refraction index, we can figure out what the outgoing angle
should be. We can rewrite the equation as:
sin(a) / n2 = sin(b)
One other point is the fact that most rays enter a
medium and leave a medium. For
example a ray enters a sheet of glass and then exits the other side of that
glass. In this diagram, the top
purple line is the incident ray entering the glass, the red line is the ray
refracted in the glass and the bottom purple line is the ray coming out of the
glass.
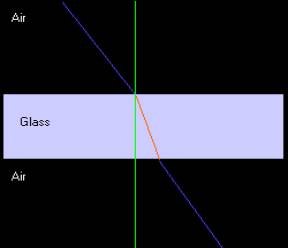
As can be seen from the above diagram the light ray
actually is parallel to the incoming light ray, but is just moved slightly
towards the normal. On the other
hand if the light ray strikes an object that is in water, then transmits to
glass and out to air, then that object contributes to the bending of the light
rays.
The reason our technique works in the above example
is that you can approximate the ray going into the glass and coming out of it by
just using on ray as shown in the following diagram:
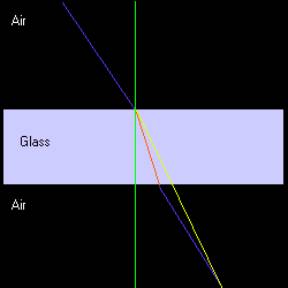
The lines above are all the same as in the previous
diagram, except for the yellow line. This line represents the refraction index
that is actually used since we are just interested in the end point of the ray.
How DirectX Calculates Reflection Vectors
R = 2(N · E) N - ESince reflection is stated in terms of the refraction formula:
R = -(a - 1)( (N · E) N - E, where a = index of refraction and a = -1 for reflection, we can substitute the refraction equation back into each vertex and give that value to the hardware for indexing into the cube maps
How
to Use Cube-Maps for the Effect
You
setup cube maps exactly the same as if you where going to reflect an object.
Now instead of using the flags, D3DTSS_TCI_REFLECTIONVECTOR, you set the
D3DTSS_TCI_PASSTHRU flag and calculate the equations for each vertex.
The hardware will interpolate the texture coordinates across the cube
map. The code sample actually
doesn't do this, because this is the default state of Direct X.
But if you wanted to set this up you would specify the following:
SetTextureStageState( 0, D3DTSS_TEXCOORDINDEX,
D3DTSS_TCI_PASSTHRU | 0);
Calculating refraction
Below is the code for calculating the refraction:
Notice that above the calculation of 1.0f/gRefractIndex
should be adjusted for minification/magnification that happens when a texture is
being used that does not map to a 1-to-1 correspondence with the object being
texture mapped.
Suggested Methods
Several papers including Paul Diefenbach's Thesis
and early work by Paul Heckbert and Pat Hanahran, suggest using the planes that
are refracting the image by use of a projection matrix that changes the angle of
view. One problem that Paul
Diefenbach notes is that using these techniques may not be possible on some
hardware because moving the projection matrix, precludes the use of the
Z-Buffer. This technique we have
described does not suffer from this limitation as it uses cube-maps to render
the scene first. The technique does
not modify the projection matrix, so the Z-Buffer can be used with this
technique.
It also might be possible to use the projection
matrix along with cube maps to automatically calculate out the values to be used
in the cube map. I've looked into
this a little, but I didn't see an obvious way to accomplish this.
Enhancements
Real world objects also reflect the environment.
There is also a critical angle refraction that says when the angles falls
between a certain point, the refraction turns into reflection.
Another enhancement would be Fresnel effects. All of these effects can be achieved. For the reflection portion, you can alpha blend between the
refraction effect and the reflection effect.
Limitations
With the
current scheme there isn't an easy way to simulate placing a pencil in a glass
of water. This technique also does
not allow internal reflections.
Conclusion
This effect is using an approximation to refraction.
You can achieve real time frame rates using this technique and the end
result is visually very good. Throughout
this document you will noticed that I did this from the perspective of ray
tracing, but you can also view this as ray casting from the eye point.
Sample
- Refraction Index 1.33 (Water)
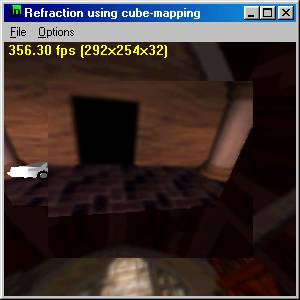 |
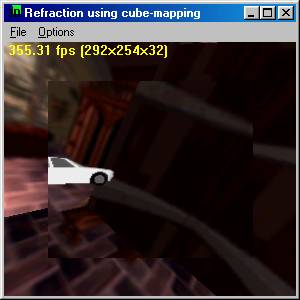 |
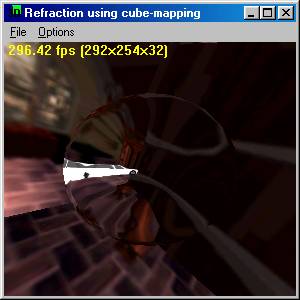 |
Sample
- Refraction Index ~= 1.5 (glass)
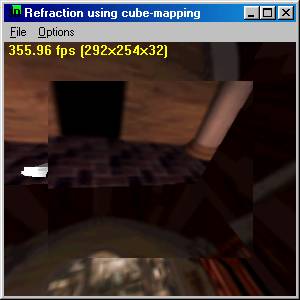 |
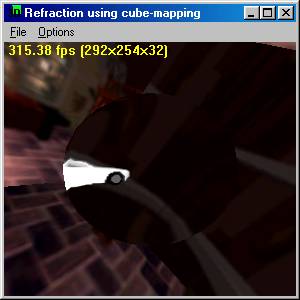 |
||||
 |
|||||
No comments:
Post a Comment